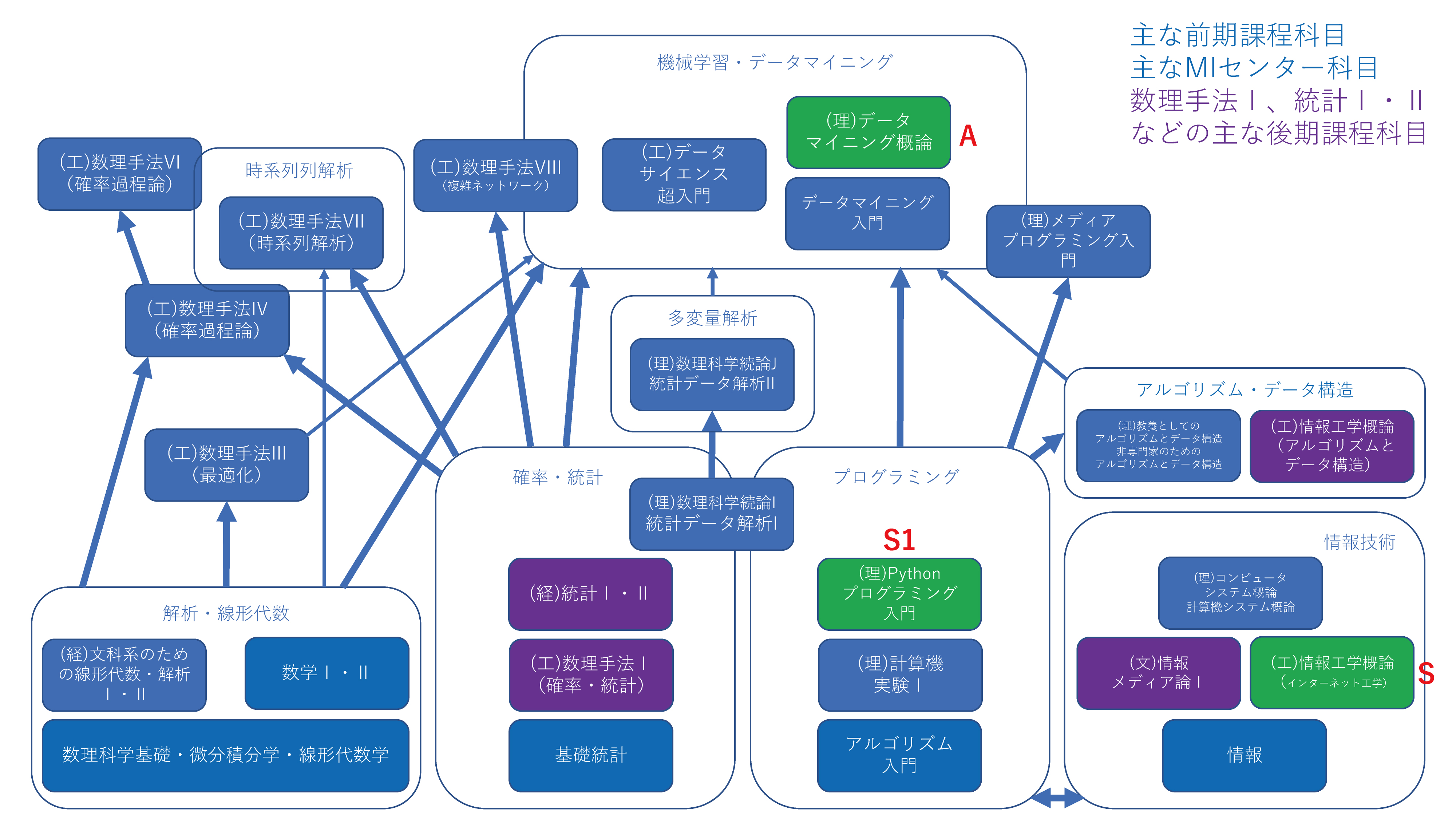
データサイエンス履修の手引き概要
データサイエンスを学ぶには、そのための基礎として、数理系科目(解析・線形代数)、統計系科目(確率・統計)、情報技術系科目、プログラミング系科目を履修する必要があります。科目系統の説明はこちら
このページでは、前期課程と後期課程の主要な科目を図示し、これらの科目間の関係を明らかにしています。さらに、機械学習・データマイニングをゴールとして、いくつかの履修パターンを示しています。
前期課程だけでも、後期課程からでも、大学院に入学してからでも、様々な方法でデータサイエンスを学ぶことができます。履修の参考にしてください。
以下の図は、それぞれの系統の主要な科目と、数理・情報教育研究センターが提供するデータサイエンス分野の科目を示しています。各講義からはより詳細な説明を表示します。
図中の科目名をクリックすると各科目の詳細な説明が表示されます。
基礎統計
開講時期:S・A
SとAの両方で同様の授業が開講されている。
前提知識
文科生も数多く履修すること、また前期課程において数学が必修ではないことから、高校の「数学Ⅱ・B」レベルを前提とする。ただし、担当教員により多少の前提知識の違いがあるので、初回の講義やシラバスで確認すること。なお、成績の優3割規定は文理別に適用される。
学修内容(要約)
高校の数学Ⅰの単元「データの分析」の内容を含む記述統計を学んだ後、データの背後に確率的なモデルを想定し、手元のデータを確率的誤差を込めて扱う推測統計を学ぶ。
確率は高校の「数学A」の単元「場合の数と確率」でも扱われるが、確率的なモデルの表現には不十分なので、推測統計を学ぶ前に確率の基礎を学ぶ。
ただし、担当教員により多少の違いがあるので、初回の講義やシラバスで確認すること。
何が出来るようになるか?
統計学はデータサイエンスの基盤となる学問分野の一つであり、例えば機械学習の複雑で高度なモデリング・解析手法に遭遇した場合でも、「基礎統計」で学ぶ基礎が理解の助けとなる。
担当教員によっては、excelやRによる統計データ解析のデモンストレーションがあるので、積極的に自分のPCや情報教育棟のPCで実践することが期待される。
次のステップ
前期課程においては、「統計データ解析Ⅰ」「統計データ解析Ⅱ」で統計ソフトウェアRを用いたデータ解析を深く学ぶことが出来る。
また「アルゴリズム入門」では、最小二乗法など基礎統計でも重要ないくつかのトピックをアルゴリズムの観点から学ぶことが出来る。
また後期課程において様々な学部で統計データサイエンス関連科目を履修する場合の基盤となる知識が身につく。
(工)数理手法Ⅷ(データ駆動科学の数理)
開講時期:A
前提知識
教養学部の理系数学の学習を前提とする
学修内容(要約)
主に経済・社会系に関する最近の data-driven な研究を紹介し、それらを理解するための数理手法を解説する。
はじめに、社会・経済現象についての物理学を可能にしつつあるデータ解析と数理・物理手法について解説する。その後、グーグル検索、国の競争力などの重要性評価の手法、統計解析とスパースモデリング、分布関数と臨界現象、最後に複雑ネットワークについて解説する。
何が出来るようになるか?
研究を進めるのに重要なこれらの数理手法の理解の⽷⼝が掴める
数学Ⅰ・Ⅱ
数理科学基礎・微分積分学・線形代数学および(経)文科系のための線形代数・解析Ⅰ・Ⅱと同様に、大学数学の標準的なもので、線形代数と微積分の基礎を学びます。
数学Ⅰ・Ⅱは前期課程の文系の選択科目で、それぞれ、SとAのどちらでも開講されています。
数理科学基礎・微分積分学・線形代数学は理系の必修科目で、併せて通年で開講されています。
(経)文科系のための線形代数・解析Ⅰ・Ⅱは、S1とS2で開講されています。
(工)データサイエンス超入門
開講時期:S1・A1
前提知識
文理を問わないが、駒場前期課程の文系向け数学科目、数学Ⅰ(1変数微積)、数学Ⅱ(ベクトル、行列の基礎)程度の数学知識は前提とする。
プログラミング経験は不要であるが、与えられたRのプログラムをノートパソコン上で動作させることができる程度のコンピュータ経験が必要。Rの初歩、たとえば、小池先生の統計データ解析Ⅰの最初の4回の講義(https://ocwx.ocw.u-tokyo.ac.jp/course_11405/で提供されている)を受講していると有益である。
機械学習、AIなどを含むデータサイエンスを今後専門専門的に履修「しない」学生、あるいは、数理・情報に関する経験が乏しい学生が学習することを配慮して、授業を行う。
学修内容(要約)
データサイエンスに関する社会状況などの周囲状況およびデータサイエンスの技術概要、特に、データサイエンスに関わる統計・機械学習の概要を講義する。講義で紹介された統計・機械学習手法を用いて、分類や予測・回帰問題をRのプログラミングにより解く。これにより、データサイエンスの概要を把握・学習し、より高度な内容への導入部とする。
何が出来るようになるか?
データサイエンスの概要、特に、主たる機械学習手法の初歩的な知識が得られる。
Rのライブラリを用いた統計・機械学習プログラミングの実行方法を習得できる。例えば、与えられたデータセットに対して、glmnetライブラリによる重回帰分析、randomForestやkernlab(サポートベクターマシーン)、nnet(ニューラルネット)などのライブラリによる分類、判別、回帰分析、予測などが行えるようになる。
次のステップ
データマイニング入門・概論と同様に、後期課程・大学院では発展的なデータサイエンスや機械学習の科目の履修が考えられる。
(理)データマイニング概論
開講時期:A
前提知識
データマイニング入門と同様。プログラミングについては(理)Pythonプログラミング入門の履修が適切である。
学修内容(要約)
データマイニング入門に加えて、ランダムフォレストやサポートベクターマシーンなどの応用手法を学ぶ。最後にニューラルネットワークやその発展としての深層学習を画像認識や言語処理などの応用を含めて学ぶ。
何が出来るようになるか?
データマイニング入門と同様。さらに、画像認識や言語処理において活用されているニューラルネットワークやその発展としての深層学習について把握できる。
次のステップ
データマイニング入門と同様。
データマイニング入門
開講時期:S
前提知識
高校数学を理解していること、プログラミングについてはアルゴリズム入門の文科クラスと同等の内容を理解しているのが望ましい。さらに、確率・統計、線形代数、解析、最適化などの数学的知識は授業内でその都度説明するが、確率・統計と解析・線形代数に関する科目を履修していることが望ましい。
学修内容(要約)
データ分析・データマイニングの基礎についてその数理統計的な背景も含めて体系的に学ぶとともに、プログラミング演習を通して実際にデータを分析するプロセスを学ぶ。
Pythonの様々なモジュールを含めプログラミングの基礎を学んだ後、記述統計や前処理、テキストデータやネットワークデータのベクトル化、教師あり学習の基礎(線形回帰やロジスティック回帰)、教師なし学習の基礎(クラスタリングや次元削減)などの手法について学ぶ。
これらの手法についてはPythonで実際に実装することで理解を深め、授業全体の最後には学習した内容を元にデータ分析のプロジェクトを行う。
何が出来るようになるか?
本授業を履修することで、Pythonを使った基本的なデータ分析ができるようになる。具体的には、テキストやグラフデータの分析、機械学習による回帰や分類などの予測、などを行うための知識とプログラミング技術を習得できる。これらは、後期課程や大学院におけるデータサイエンス、機械学習、人工知能、などの関連授業の基礎となる知識である。
次のステップ
本授業履修後に学べるより発展的な授業として、深層学習の基礎なども内容を扱う(理)データマイニング概論がある。また、その他にも後期課程・大学院では発展的なデータサイエンスや機械学習の科目として、(情理)データサイエンス、(工)統計的機械学習、(情理)機械学習の数理、(情理)知能機械情報学、などがある。
また、深層学習を中心とした先端の人工知能について学べる科目として、(理)知能システム論、(情理)先端人工知能論、(工学系)深層学習、などがある。その他に興味に応じて、言語・音声情報処理、自然言語処理、生物データマイニング、バイオインフォマティクス、などの応用分野の科目を学ぶことができる。
(理)メディアプログラミング入門
開講時期:S2・A2
前提知識
Pythonプログラミング入門を受講しているか、もしくは同等程度のプログラミング力があることを前提としている。
学修内容(要約)
音の回では人間の聴覚の仕組みや音の収録・記録、周波数解析・音の可視化技術等について学ぶ。テキスト(自然言語)の回では、小説やWikipedia記事を題材に、形態素解析や言語モデル、トピック分析や文書検索、文書間類似度・単語埋め込み(Word embedding)等について学ぶ。
画像の回では人間の視覚の仕組みや画像のデータ表現、基礎的な画像処理から深層学習による画像認識等について学ぶ。最後に、メディア情報を収集する手段であるウェブスクレイピングやWebAPIについて学ぶ。
何が出来るようになるか?
音やテキスト、画像などのメディア情報を自分で分析できるようになる。また、機械学習をメディア情報に適用する際に必要となる前処理(特徴ベクトル化)を学ぶことができる。
次のステップ
データマイニング入門・概論と同様に、この授業を受講した後は、より高度な機械学習やアルゴリズムの学習に進んでいくとよい。
(工)数理手法Ⅵ(確率過程論)
開講時期:A
前提知識
測度論や積分論等の数学の専門的知識は前提としない。
学修内容(要約)
時間とともに変化する不確実な現象を記述し理解するには、確率過程論が重要な道具として用いられる。
数理手法Ⅵでは、数理手法Ⅳに続き、離散時間の確率過程論の講義を行った後、連続時間の確率過程の理論について講義を行う。
何が出来るようになるか?
確率過程論の理解を得ることができる。
時間と共に変化するランダムな事象に対し、様々な確率計算が可能になる。特にブラック・ショールズ理論を簡易化したものを理解できるようになる。(数理手法Ⅳ)
マルチンゲール、マルコフ過程、ブラウン運動、確率微分方程式などの確率過程の理論の基礎を理解できる。経済・数理ファイナンスにおける重要な理論である、ブラック・ショールズ理論を理解できるようになる。(数理手法Ⅵ)
(工)数理手法Ⅶ(時系列解析)
開講時期:S
前提知識
前期課程における数学の基礎科目(「数理科学基礎」「微分積分学」「線型代数学」「数学Ⅰ」「数学Ⅱ」)や総合科目F系列「基礎統計」、後期課程の各学部において数理データサイエンス関連科目を習得した学生は、本講義の内容をより深く理解することができる。
ただし、そのような科目を履修していることを前提とはしない。各専門分野における具体的な課題やそのために解析したい時系列データがあればなお良い。
学修内容(要約)
時間とともに変動する現象を記録したデータである時系列データに基づき、複雑な現象を理解し、予測、制御や意思決定を行うための時系列モデリングの方法とその応用について講義する。
何が出来るようになるか?
時系列データの前処理や特徴の可視化ができる。
統計的モデリングの方法、線形・定常時系列モデル、状態空間モデルおよび非線形・非ガウス型モデルに習熟して、現実の問題に対応して適切なモデリングができる。
次のステップ
後期課程や大学院における時系列データを用いた関連科目が履修できる。
(工)数理手法Ⅳ(確率過程論)
開講時期:S
前提知識
測度論や積分論等の数学の専門的知識は前提としない。
学修内容(要約)
時間とともに変化する不確実な現象を記述し理解するには、確率過程論が重要な道具として用いられる。
数理手法Ⅳでは、離散時間の確率過程論、特にマルチンゲール理論に関しての講義を行う。
何が出来るようになるか?
確率過程論の理解を得ることができる。
時間と共に変化するランダムな事象に対し、様々な確率計算が可能になる。特にブラック・ショールズ理論を簡易化したものを理解できるようになる。(数理手法Ⅳ)
マルチンゲール、マルコフ過程、ブラウン運動、確率微分方程式などの確率過程の理論の基礎を理解できる。経済・数理ファイナンスにおける重要な理論である、ブラック・ショールズ理論を理解できるようになる。(数理手法Ⅵ)
統計データ解析Ⅱ/(理)数理科学続論J
開講時期: S(統計データ解析Ⅱ)・A((理)数理科学続論J)
統計データ解析Ⅱと(理)数理科学続Jは同様の内容である。
前提知識
基礎科目(「数理科学基礎」「微分積分学」「線型代数学」「数学Ⅰ」「数学Ⅱ」)や総合科目F系列(「基礎統計」「統計データ解析Ⅰ」)を習得した学生は、本講義の内容をより深く理解することができる。ただし、そのような科目を履修していることを前提とはしない。
学修内容(要約)
統計ソフトウェアRの説明の後、高次元大規模データに潜む相関構造を発見し計量する多変量解析、および時系列データの基本的な解析法を学ぶ。
何が出来るようになるか?
重回帰分析、主成分分析、判別分析といった、やや高度な統計手法の運用とデータハンドリングに習熟出来る。
微分積分学、線型代数学等の前期課程数学と連携し、数理科学的側面を意識しながら、実験を介して統計手法の合理性と体系が理解できるようになる。
次のステップ
後期課程において様々な学部で統計データサイエンス関連科目を履修する場合の基盤となる知識が身につく。
(工)数理手法Ⅲ(最適化)
開講時期:A
前提知識
線形代数および微分・積分の基礎を前提とする。
学修内容(要約)
最適化とその応用について講述する。最適化(数理計画)とは、意思決定のための数理手法の一つである。最適化では、与えられた条件を満たす解のうち、ある関数を最小(または最大)にするものを求める。工学における多くの問題が、このような最適化問題として定式化できる。また、データサイエンスのさまざまな手法に、最適化の考え方や解法が用いられている。この講義では、最適化におけるいくつかの基本的な問題(非線形計画、凸計画、ネットワーク最適化、近似解法、整数計画)を取り上げ、それらがもつ性質と解法とを説明するとともに、それらの応用を紹介する。特に、正則化付き回帰分析やクラスタリングの手法などを、最適化の観点から講述する。
何が出来るようになるか?
最適化の基本的な手法を習得できる。
次のステップ
(経)文科系のための線形代数・解析Ⅰ・Ⅱ
数学Ⅰ・Ⅱおよび数理科学基礎・微分積分学・線形代数学と同様に、大学数学の標準的なもので、線形代数と微積分の基礎を学びます。
数学Ⅰ・Ⅱは前期課程の文系の選択科目で、それぞれ、SとAのどちらでも開講されています。
数理科学基礎・微分積分学・線形代数学は理系の必修科目で、併せて通年で開講されています。
(経)文科系のための線形代数・解析Ⅰ・Ⅱは、S1とS2で開講されています。
統計データ解析Ⅰ/(理)数理科学続論I
開講時期:A(統計データ解析Ⅰ)・S((理)数理科学続論I)
統計データ解析Ⅰと(理)数理科学続論Iは同様の内容である。
前提知識
基礎科目(「数理科学基礎」「微分積分学」「線型代数学」「数学Ⅰ」「数学Ⅱ」)や総合科目F系列「基礎統計」を習得した学生は、本講義の内容をより深く理解することができる。ただし、そのような科目を履修していることを前提とはしない。
学修内容(要約)
受講者が統計ソフトウェアを用いた実験によって確率的現象に慣れ、統計推測法の意味を理解し、データ解析の方法を実習する。
統計ソフトウェアRの使い方を学んだあと、シミュレーションによってランダムネスと極限定理を体験する。
基本的な確率分布について学習したのち、推測統計における基礎的な推定・検定法、および分散分析の方法を、データ処理を通じて実習する。
何が出来るようになるか?
統計手法の運用とデータハンドリングについて習熟出来る。
次のステップ
前期課程で開講される「統計データ解析Ⅱ」では、高次元で大規模なデータの解析方法が学べる。
また後期課程において様々な学部で統計データサイエンス関連科目を履修する場合の基盤となる知識が身につく。
(経)統計Ⅰ・Ⅱ
開講時期:A1((経)統計Ⅰ)・A2((経)統計Ⅱ)
経済学部2Aの科目であり、週に2回ずつ行われる。駒場で開講されている。
前提知識
文科系の数学の基礎科目(特に「数学Ⅰ」レベルの微積分)を仮定する。講義内で適宜復習を行うが、1年次に数学を履修していない方にはあらかじめ2年次に履修することを勧めている。統計学の知識は仮定しない。また、講義の中でRを用いたデータ解析についてもふれるが、プログラミングの知識・経験は仮定しない。
学修内容(要約)
この講義では受講者が主に経済学・経営学などの分野に関心があることを考慮して、統計学の基礎について講義する。
技術的・数理的側面(記述統計と数理統計)の解説も省略せずに行い、進んだ内容の理論・応用の学習の準備となるように努める。
何が出来るようになるか?
経済学部進学後、本郷で開講される選択必修科目や演習(ゼミ)において前提となる統計学の基礎知識を習得できる。
統計検定二級相当の数理統計の知識が身につく。
次のステップ
経済学部進学後は「計量経済学Ⅰ、Ⅱ」「応用統計」「数理統計Ⅰ、Ⅱ」「経済データ分析」など多くの上級科目が履修できる。
経済学部の学生はさらに、統計副専攻の教員が開講する演習・少人数講義を履修できる。また、一部の大学院科目は「上級数理統計I,II」「上級計量経済学I,II」として学部生でも履修することができる。
(工)数理手法Ⅰ(確率・統計)
開講時期:A
工学部2Aの科目であり、駒場で開講されている。
前提知識
微積分、線形代数等の統計分析に必要な数学の基礎知識を有すること。
教養学部の「基礎統計」を履修したか、同等程度の確率・統計の知識があることが望ましい。
「基礎統計」を履修していない学生は、東大教養学部編「統計学入門」などで、その基礎を復習視しておくこと。
学修内容(要約)
確率・統計の基礎について学ぶとともに、Excelを用いた統計分析について演習を行う。
扱う項目は、確率・統計の標準的・基礎的項目である。具体的には、確率・確率分布・確率変数、データの整理と記述統計、大数の法則と中心極限定理、標本分布、推定と検定、回帰分析を扱う。
何が出来るようになるか?
Excelを用いて基本的な統計分析を行えるようになる。
(理)Pythonプログラミング入門
開講時期:S1・夏集中・A1
1ターム(1単位)の授業が、S1・夏集中・A1に開講されている。さらに、S1とA1では、複数曜日に開講されている。
前提知識
プログラミングの関する経験は一切仮定しないが、パソコンの操作(ウェブ、ファイルシステム、エディタなど)についてはある程度慣れている必要がある。
自分のパソコンにPythonの処理系をインストールするか、クラウド環境をブラウザで利用できるパソコンやタブレットを用意する必要がある。
学修内容(要約)
実用的なプログラムを書けるようなることを目的としているので、ファイル入出力やモジュールなども扱う。オブジェクト指向や関数プログラミングについても簡単に触れる。さらに、最終回はデータマイニングや機械学習への入門となっており、ライブラリを用いたデータ分析について学ぶ。
1タームの授業であり、多くの履修者を想定しているため、反転授業として進められる。履修者はあらかじめJupyter Notebookの教材を自習し課題を提出する。各回の授業では教員やTAに質問しながら、その回の演習課題を行います。
何が出来るようになるか?
Pythonのプログラムをある程度自由に書けるようになるとともに、特にデータサイエンスのための実用的なプログラムがPythonで書けるようなる。
次のステップ
(理)データマイニング概論、(理)メディアプログラミング入門など、データサイエンスの科目、さらに、機械学習(特に深層学習)に関する科目の履修が容易になる。
より効率的なプログラムを書くにはアルゴリズムとデータ構造を学ぶことが望ましい。 (理)教養としてのアルゴリズム入門、(工)情報工学概論(アルゴリズムとデータ構造)など、アルゴリズムとデータ構造を学ぶ授業も多い。
(理)計算機実験Ⅰ
開講時期:S
前提知識
特になし。
学修内容(要約)
UNIX操作、リモートログインの演習の後、C言語プログラミングについて、ライブラリの利用まで学ぶ。その後、数値誤差、数値微分、ニュートン法、常微分方程式の初期値問題、Euler法・Runge-Kutta法、シンプレクティック積分法、偏微分方程式の境界値問題、連立一次方程式の解法、Gaussの消去法・LU分解、反復解法、行列計算、密行列の固有値問題、疎行列の対する反復法、特異値分解、最小二乗法による回帰分析について学ぶ。
何が出来るようになるか?
理論・実験を問わず、学部〜大学院〜で必要とされる現代的かつ普遍的な計算機の素養が身につく。
アルゴリズム入門
開講時期:A
理科クラス指定科目および文科向け選択科目が提供されている。文科の学生が理科クラス指定科目を履修することもできる。文科向け選択科目では文科の学生のみ履修できる。
前提知識
プログラミングやアルゴリズムに関しても基礎から解説されるので、科目「情報」の知識をほとんど前提としていない。ただし、パソコンの基本的な操作(ウェブ、ファイルシステム、エディタなど)については慣れている必要がある。
学修内容(要約)
Pythonをプログラミング言語として、プログラミングの基礎、具体的には、主要な制御構造、関数定義、リストや辞書などのデータ構造を学びながら、探索、平均・分散・p値などの統計処理、常微分方程式・拡散方程式のシミュレーション、モンテカルロシミュレーション、連立一次方程式の求解、線形回帰などをプログラミングの題材として学ぶ。計算量についても簡単に触れている。
何が出来るようになるか?
Pythonのプログラムをある程度自由に書けるようになるとともに、シミュレーションやデータ分析のための基本的なプログラミングを習得できる。
プログラミングが未経験であっても、基本的なプログラムが書けるようになるので、是非とも履修して欲しい。この科目を履修しておけば、他のプログラミング言語を学ぶ際にもハードルは低くなる。
次のステップ
データマイニング入門、(理)データマイニング概論、(理)メディアプログラミング入門など、データサイエンスの科目、さらに、機械学習(特に深層学習)に関する科目の履修が容易になる。
プログラミングについてより深く学びたい場合や他のプログラミング言語を学びたい場合は、前期課程では計算機プログラミングを履修すするのがよい。
より効率的なプログラムを書くにはアルゴリズムとデータ構造を学ぶことが望ましい。非専門家のためのアルゴリズムとデータ構造、(理)教養としてのアルゴリズム入門、(工)情報工学概論(アルゴリズムとデータ構造)など、アルゴリズムとデータ構造を学ぶ授業も多い。
計算機プログラミング(非専門家のためのアルゴリズムとデータ構造)
開講時期:A
前提知識
特にない。
学修内容(要約)
アルゴリズムとは「問題」を解くための手順であり、データ構造は計算機(コンピュータ)上においてアルゴリズムを実行する際にデータを保持するための方法である。これらは計算機科学の基礎をなす学問分野である一方、計算機科学とは全く異なる分野においても陰に陽に重要な役割を果たしていることが少なくない。
本授業では、文理問わず後期課程進学後に計算機科学「以外」の学問を修める学生を対象とし、進学後に出会うであろうアルゴリズムとデータ構造に関する事柄について学ぶ。具体的には、実際にこれらが他分野(例えば、言語学、生物学など)において関わってくる場面を例示しつつ、それらの機能や仕組みについて学ぶ。
何が出来るようになるか?
計算機科学「以外」の学問分野において用いられているアルゴリズムとデータ構造について学ぶことで、その仕組みや働きについて理解を深めることができる。実際に各分野で必要となるプログラムを作成する際に活用できる。
各回の課題に取り組むことで論理的思考力を鍛えられる。
次のステップ
本授業は、アルゴリズムとデータ構造の理論について学ぶが、プログラミングなどでこれらを実際に用いるには、実践的な内容を学ぶ授業(例えば、アルゴリズム入門)を履修したり、特定のプログラミング言語に特化したアルゴリズムとデータ構造を扱った書籍を読んだりするのがよい。
(理)教養としてのアルゴリズムとデータ構造
開講時期:S2
前提知識
Pythonプログラミング入門において学習する程度のPythonの知識を必要とする。また、授業の際には各自がノートパソコンを持って参加することを想定している。
学修内容(要約)
アルゴリズムとは、「問題」を解くための手順であり、データ構造は計算機(コンピュータ)上においてデータを保持するための方法である。これらは計算機科学の分野において基本的かつ重要な役割を果たしている。本授業ではアルゴリズム及びデータ構造の基礎について学ぶとともに、Python言語を通じてその機能を体験することを主眼とする。
何が出来るようになるか?
基礎的なアルゴリズムとデータ構造の仕組みや働きについての理解が深まる。また、それらをある程度使いこなして、計算機上において解決すべき問題に対して、Pythonを利用して対処できるようになる。
次のステップ
より高度な理論、もしくは実践的な内容を扱った授業を履修したり、アルゴリズムとデータ構造を扱った書籍を読むなどしたりするとよい。
また、Pythonを用いた手続きについてより理解を深めるという観点からは、データマイニング概論やメディアプログラミング入門などを履修することを勧める。
(工)情報工学概論(アルゴリズムとデータ構造)
開講時期:S
前提知識
特にない。
学修内容(要約)
現代のあらゆる活動において情報技術の重要性は増すばかりである。そしてアルゴリズムはその情報技術の根幹をなす。効率的なアルゴリズムの実装には適切なデータ構造は欠かせない。本講義ではアルゴリズムとデータ構造の基礎を紹介する。
具体的には、アルゴリズムの記述、アルゴリズムの正当性、アルゴリズムの性能と計算複雑度、再帰アルゴリズム、分割統治法、グラフ理論入門とグラフ探索、有向グラフと最短路問題など、バケット、ハッシュ、ヒープ 、動的計画法、ネットワークフロー、貪欲アルゴリズム、計算問題の難しさの測り方 、計算困難問題に対するアプローチについて学ぶ。
何が出来るようになるか?
典型的な問題に対するアルゴリズムを理解し、類似の問題に対しては適切なアルゴリズムを適用できるようになる。
また、初めて見る問題に対しても、ある程度適切なアルゴリズムを設計できるようになる。
計算機システム概論/(理)コンピュータシステム概論
開講時期:A(計算機システム概論・S1((理)コンピュータシステム概論)
計算機システム概論は2単位、(理)コンピュータシステム概論は1単位であるが、内容は同様である。
前提知識
受講にあたっては PC 利用能力以外は特に前提を設けていない。
プログラミングに関する知識はあればよいが、講義中に示すサンプルプログラムなどを通じて理解を進めることができる。ただし、プログラミングが全くできないと履修は不可能なので、アルゴリズム入門やPythonプログラミング入門などをあらかじめ履修していることが望ましい。
(理)コンピュータシステム概論では個人の持ち込み PC を想定している。
学修内容(要約)
Web サービスの提供を想定しそれに必要な知識・技術を学ぶとともに、実践的な演習を通じてスキルの獲得方法を学ぶ。
ソフトウェア構成管理の説明の後、Pythonプログラミングについて概観した後、サーバ管理・遠隔ログイン、コンピュータの構成・クラウドサービス、Web サービスの基本、データベース、セキュリティについて学び、最後に実際のWebサービスの構築を行う。
(理)コンピュータシステム概論では、授業回数の関係から一部の内容を自習としている。
何が出来るようになるか?
コンピュータを利用した情報サービスの知識・スキルはあらゆる分野の専門家に求められているが、情報分野を専門としないものにとっては自身の専門分野に加え、サービス提供に必要な専門知識を体系的に学習することは時間的制約から厳しい。この講義では、情報サービスの構築に必要な実践的な知識・スキルを習得できる。同時に、サービスの提供に必要な知識を効率的に獲得できるようになる。
(工)情報工学概論(インターネット工学)
開講時期:S
前提知識
特にない。
学修内容(要約)
インターネットシステムの構造、要素技術、ビジネスモデルを概観し、デジタルネットワークのアーキテクチャと概要を理解する。具体的には、サイバーセキュリティ、インターネットの概略とアーキテクチャ・デジタル、ネットワークレイヤ、トランスポートレイヤ、物理・リンクレイヤ 、DNS・検索サービス、電子メール・コンテンツ、WWW(World Wide Web)、P2P(Peer-to-Peer)システム、情報通信に関するガバナンスについて学ぶ。
何が出来るようになるか?
情報通信ネットワークの要素技術の位置づけを全体のアーキテクチャの中のものとして把握し、専門の講義で展開される個別の要素技術の必要性と役割を把握できる。
情報
開講時期:S
文科理科を問わない必修科目である。
前提知識
特にない。この科目で扱う内容の多くは、高等学校の情報科でも学ぶこととなっているが、高等学校で十分に学んでいない学生にも配慮し、前提知識なしで授業が行われる。
学修内容(要約)
情報システムをはじめとする情報技術の基礎から、記号、メディア、ユーザインタフェースなどについても触れながら、さらに、著作権、プライバシー、情報セキュリティ、ソーシャルネットワークなどの情報社会・情報倫理に関することまで、情報分野の基礎について幅広く学ぶ。情報教育等の演習室において、演習を主とする授業が行われる。
何が出来るようになるか?
デジタル化、情報量、符号化、数の表現、アルゴリズムの考え方、コンピュータアーキテクチャ、情報通信ネットワーク、情報システムなど、データサイエンスや計算科学などで活用される情報技術の基礎を把握することができる。
また、情報教育等の演習室で授業を行うので、パソコンの基本的な操作(ウェブ、ファイルシステム、エディタなど)を習得できる。
次のステップ
担当教員によっては、簡単なプログラミング演習を数回行うこともあるが、この授業では本格的なプログラミングは行わないので、アルゴリズム入門の履修を強く勧める。
情報技術について、前期課程では計算機システム概論などを履修することができる。
情報メディア論Ⅰ
開講時期:S
前提知識
電子工学や情報科学の基礎知識は必要としないが、コンピュータに関するリテラシーレベルの知識を持っていることが望ましい。
学修内容(要約)
本講義ではインターネットの仕組みや関連する技術を扱う。主にインターネットの基盤的なプロトコル群であるTCP/IPについて解説する。様々なネットワークが相互に接続して構成されるインターネットにおいてどのように通信が行われているのか、Webブラウザによるサイトの表示 (HTTP) やメールクライアントによる電子メールの送受信(SMTP・POP・IMAP)はどのように行われているのか、またネットワークにおけるセキュリティ技術などについても取り扱う。
何が出来るようになるか?
技術的な知識を学ぶことでインターネットをただ使うだけでなく、その動作を理解できるようになる。
数理科学基礎・微分積分学・線形代数学
数学Ⅰ・Ⅱおよび(経)文科系のための線形代数・解析Ⅰ・Ⅱと同様に、大学数学の標準的なもので、線形代数と微積分の基礎を学びます。
数学Ⅰ・Ⅱは前期課程の文系の選択科目で、それぞれ、SとAのどちらでも開講されています。
数理科学基礎・微分積分学・線形代数学は理系の必修科目で、併せて通年で開講されています。
(経)文科系のための線形代数・解析Ⅰ・Ⅱは、S1とS2で開講されています。
上図において、青の科目は前期課程科目もしくは数理・情報教育研究センターが提供する科目であり、広く全学に開かれています。数理・情報教育研究センターの提供する科目もいずれかの学部で開講されており、(工)などの印が付けられています。紫の科目は後期課程で開講されている科目で、それらの中でも典型的なものが示されています。これらの科目にも(工)などの印が付けられています。これらの科目は必ずしも広く全学に開かれているわけではありませんが、同様の科目が他の学部でも開講されています。
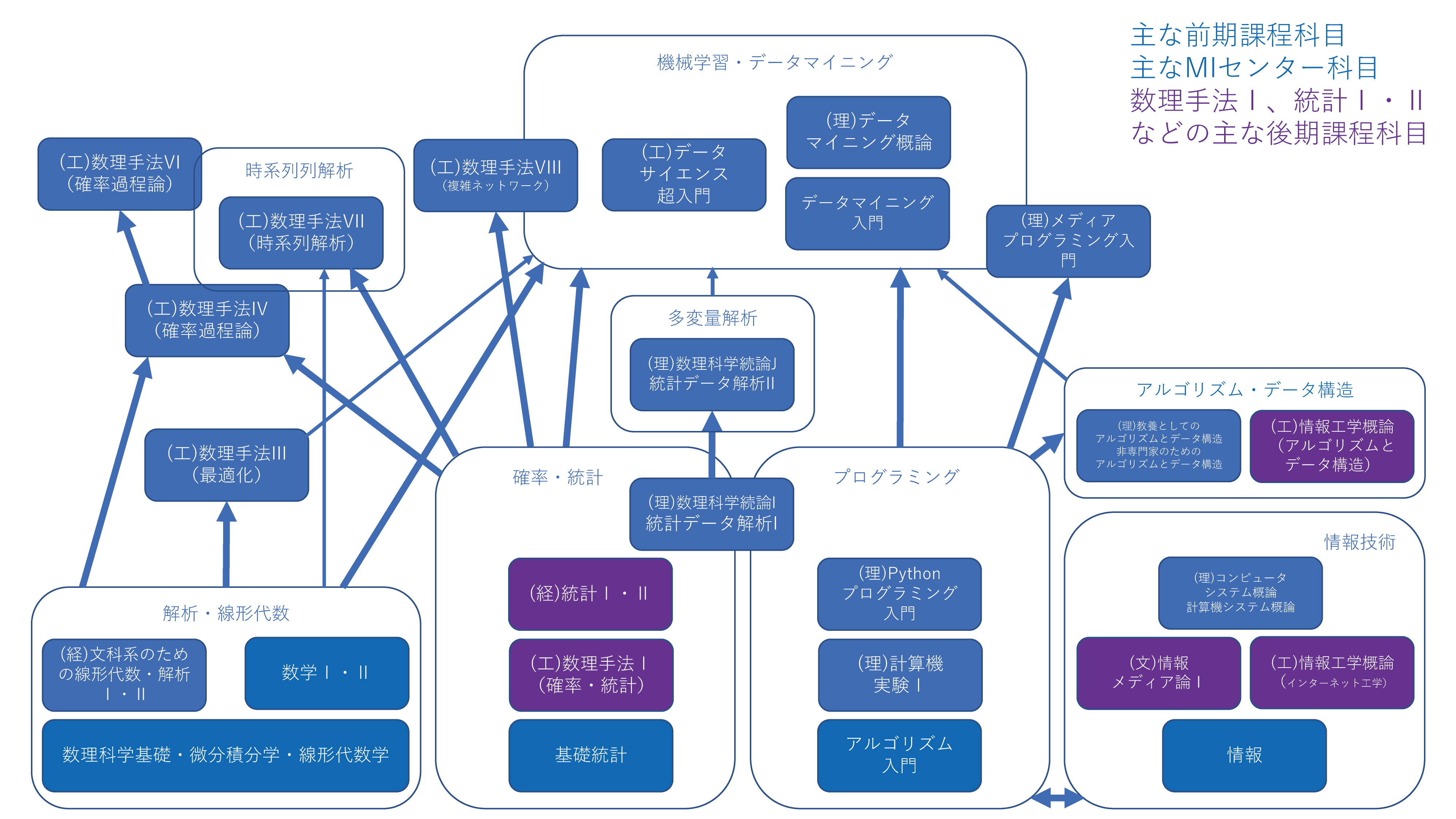
履修パターン例
以下では、機械学習・データマイニングをゴールとして、いくつかの履修パターンを示します。(なお、データマイニングはデータサイエンスと同義に用いられることが多くなっていますが、ここではより狭く、機械学習とそのための前処理や視覚化などのデータ処理を意味しています。)
文科生が後期課程のみで学ぶ
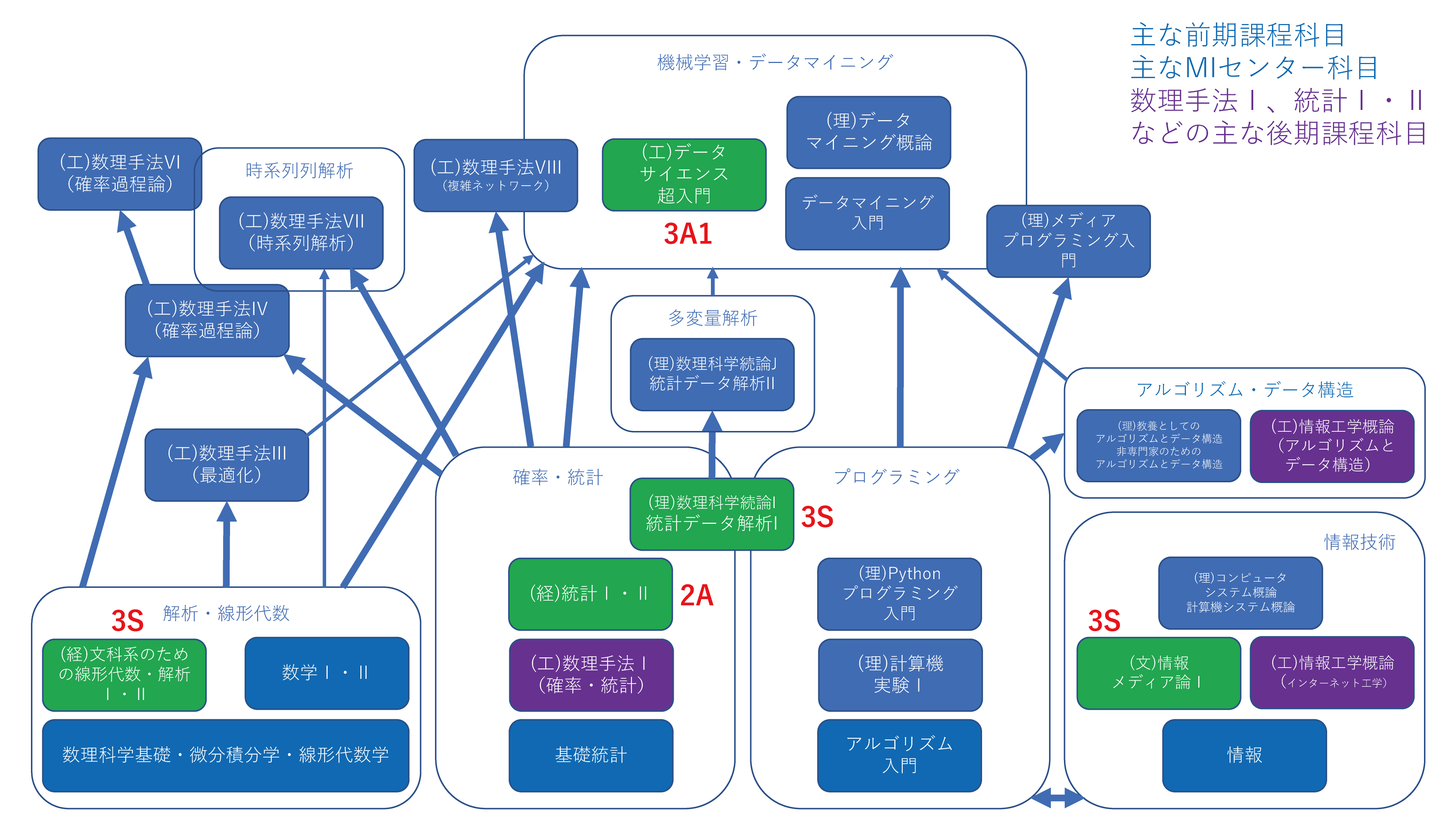
理科生が前期課程のみで学ぶ
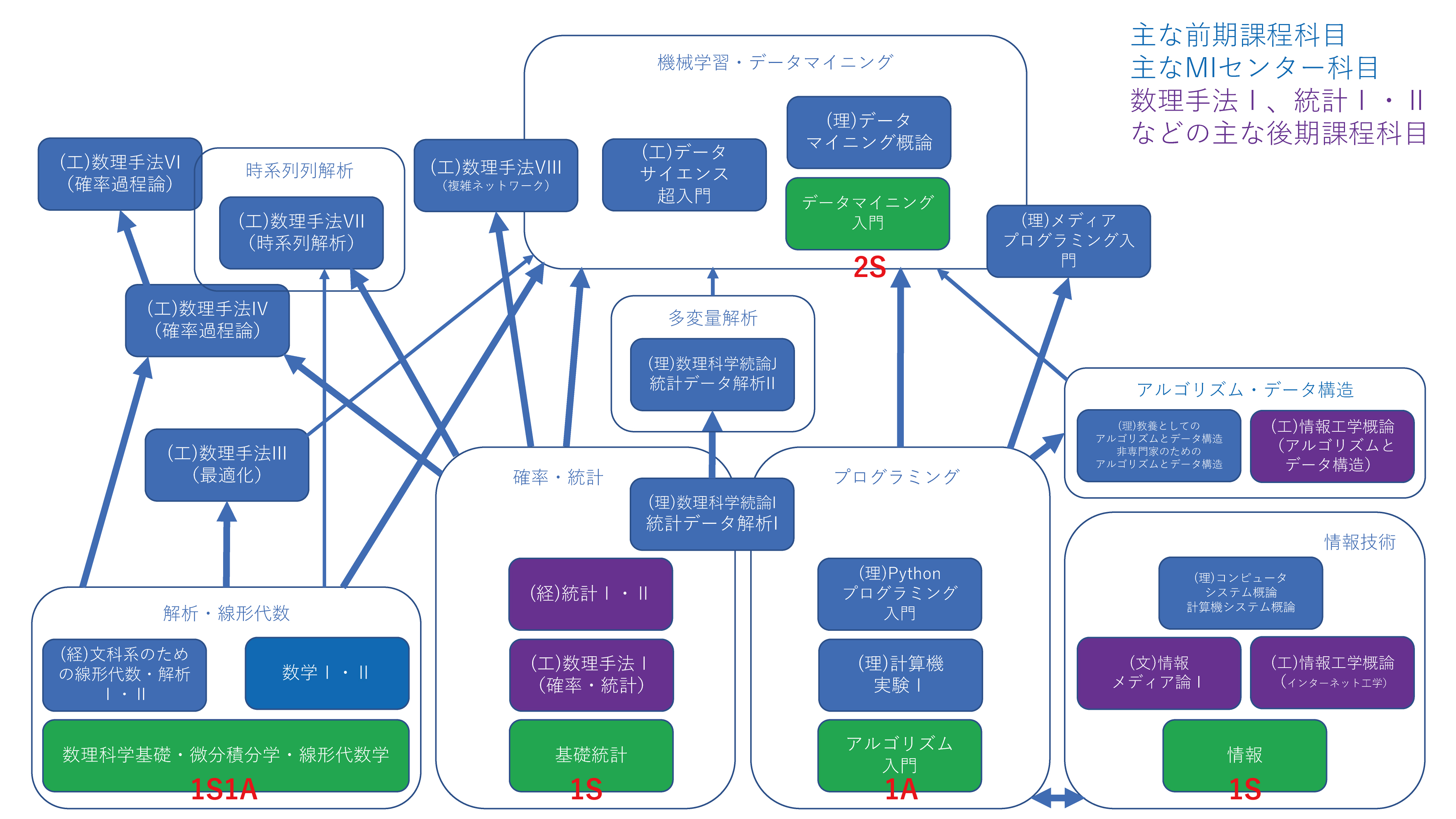
数理系と統計系の素養がある大学院生が学ぶ